11.19 Mon.
用并查集算法做上周的第三题:

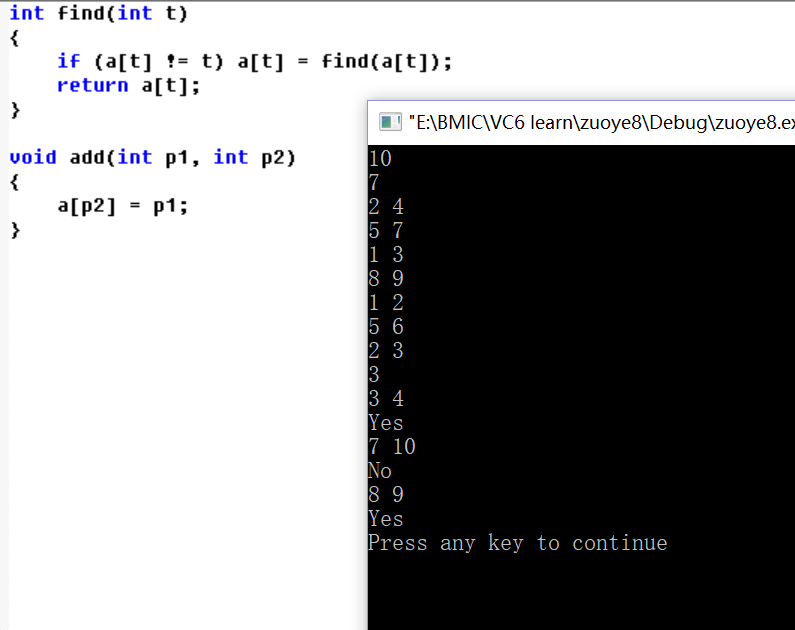
思路:使用到并查集的算法。对于每个人建立一个集合,初始化集合元素表示的其本身,每给出一个关系是就将两个集合合并,每次提问若两者属于同一个集合则表示有关系。
第二行定义的数组为全局参量,因为下面调用函数中也含有该数组部分,所以该数组不能为局部变量。局部变量在其他函数中不能被使用。
p1=find(x);p2=find(y);这两行调用find函数。
若该元素不等于本身则再次利用find函数返回上一层再进行判断其是否为本身,直到其等于本身,可以用此元素表示所有跟它有关系的元素的集合:
例:
1-2-3-4
i=1时,a[1]不等于1,则a[1]=find(a[1])
i=2时,a[2]不等于2,则a[2]=find(a[2])
i=3时,a[3]不等于3,则a[3]=find(a[3])
i=4时,a[4]等于本身,停止,此时a[1]=4,a[2]=4,a[3]=4,a[4]=4
所有跟4有关系的都可以用4来表示
add函数用来合并:若两个集合有联系则令一个集合中的元素等于另一个集合名,合并成一个集合
最后一个for循环查找,输入两个数判断是否为一个集合内,若是则表示有关系。
11.20 Tues.
尝试用前缀和的方法写上周第二题: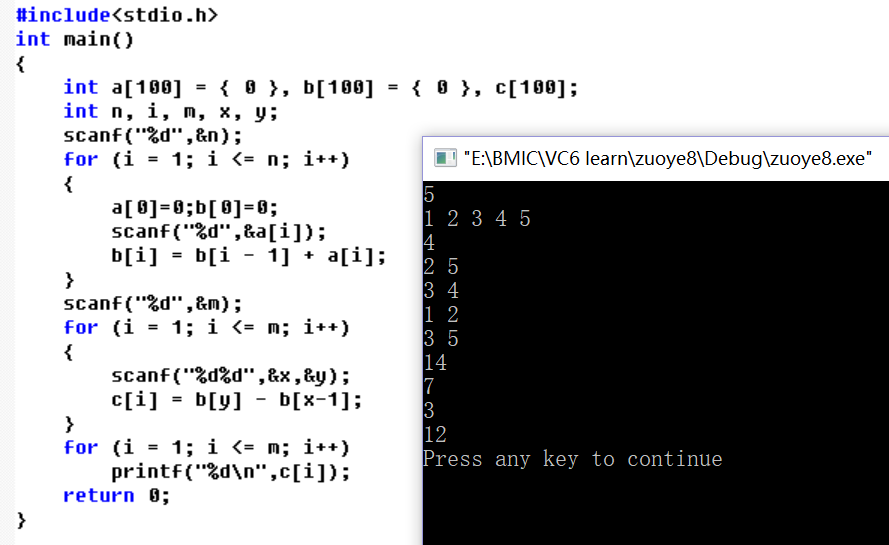
思路:前缀和
a数组下标 : 0 1 2 3 4 5
a数组存输入的数字 : 1 2 3 4 5
b数组存总和 : 1 3 6 10 15
(从下标0开始) S1 S2 S3 S4 S5
(S1表1;S2表1+2;S3表1+2+3···)
第二个for循环输入x,y,在a数组中从a[x]开始累加直到b[y],因为上面S总和中包含的有本身,所以应b[y]-b[x-1],b[x-1]表示x前面数字之和。差就为所求的区间数字之和。
11.24 Sat.
作业:
第三题: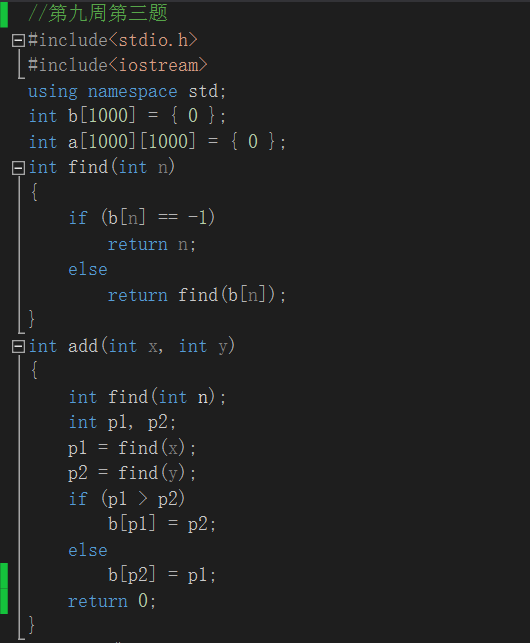
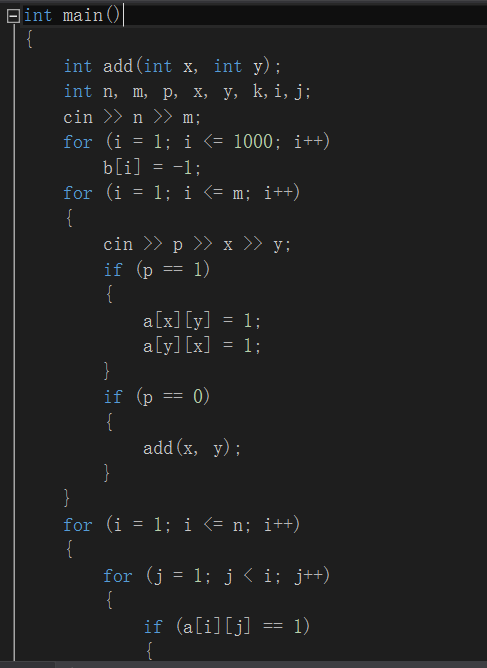
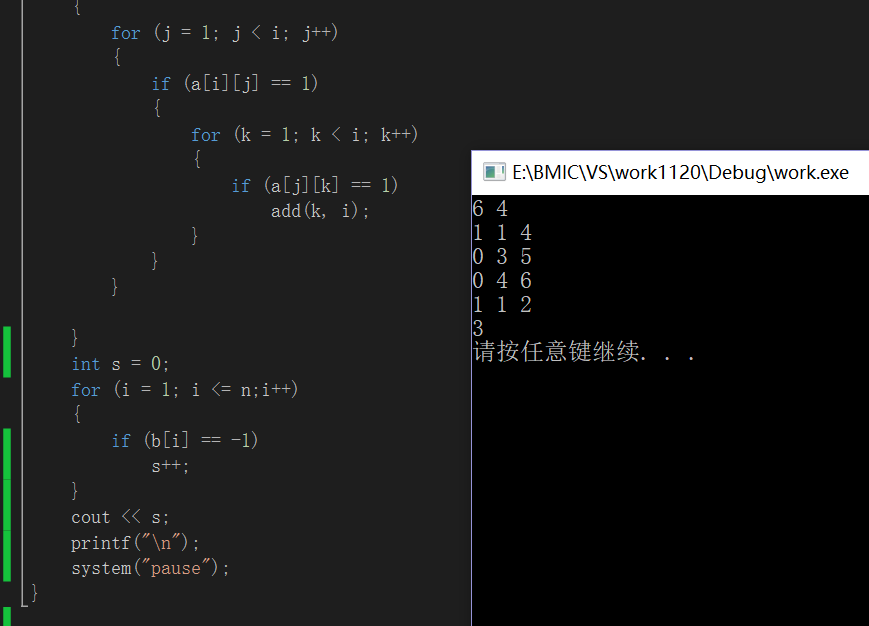
第三题用到并查集思想。思路:m条有关n个人的信息,p=1时为敌对关系,p=0时为同伙关系。在这m条信息中可以先做筛选:将同伙关系的聚集在一起放入一个集合内;因为这时每对敌对关系不确定其中的人是否与别人存在敌对关系可以合并,所以为敌对关系的先以每对的方式记录下来。(例:p,x,y=0 3 5则将3.5放入一个集合内{3,5},p,x,y=0 2 5则{2,3,5},p,x,y=1 1 4则记录下1-4位敌对关系)
接着,对每对关系的人做处理:
一开始我利用一维数组存储其敌对关系计算时会出现重复计算的情况(例:1-4存为a[1]=1,a[4]=1;1-2存为a[1]=1,a[2]=1;这时在循环判断的时候容易混乱不能确定同伙关系的两个人是谁)
后来我尝试用二维数组记录敌对关系:(主函数中第三个for循环)
1 | 2 | 3 | 4 | |
1 | 1 | 1 | ||
2 | 1 | |||
3 | ||||
4 | 1 |
“1”的位置则表示该坐标的两位数有敌对关系。为了防止重复计入,查找时只需找出单方指向的敌对人,限制条件为i<=n,j<i,当碰到为1的情况则查看这两个人是否跟别人存在有敌对关系,这里k<i避免查找到1-2之后再次记录2-1的情况。
add函数“路径压缩”
把 0,2,5 和 0,3,5 这种情况归属到一个集合内,令a[3]=2,a[5]=2
开始时可以先初始化一个数组令其每个数都为-1,若有同伙则进行路径压缩将其代表赋值给其他人,单独成团的则仍为-1,输出时总和有多少个-1就可以。
寻找根节点:
若往上查找为-1则该团头目就为这个人,其他的人跟随头目。但他们的值不是-1,是那个人的数字
第一题:
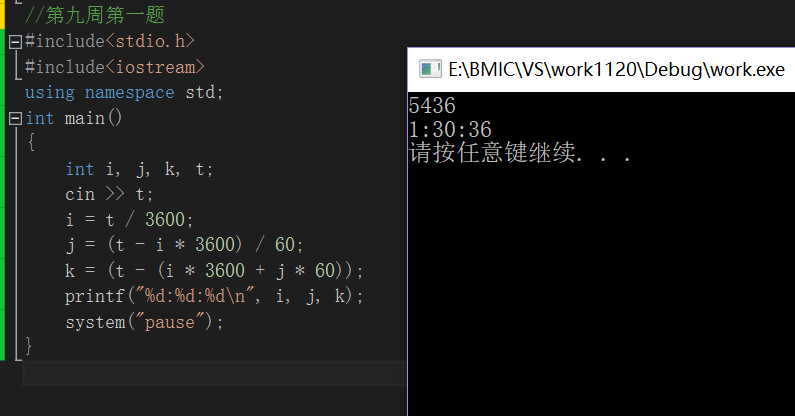
第一题利用公式计算出时,分,秒分别利用i,j,k存放,输出格式注意一下用:隔开。
第二题:
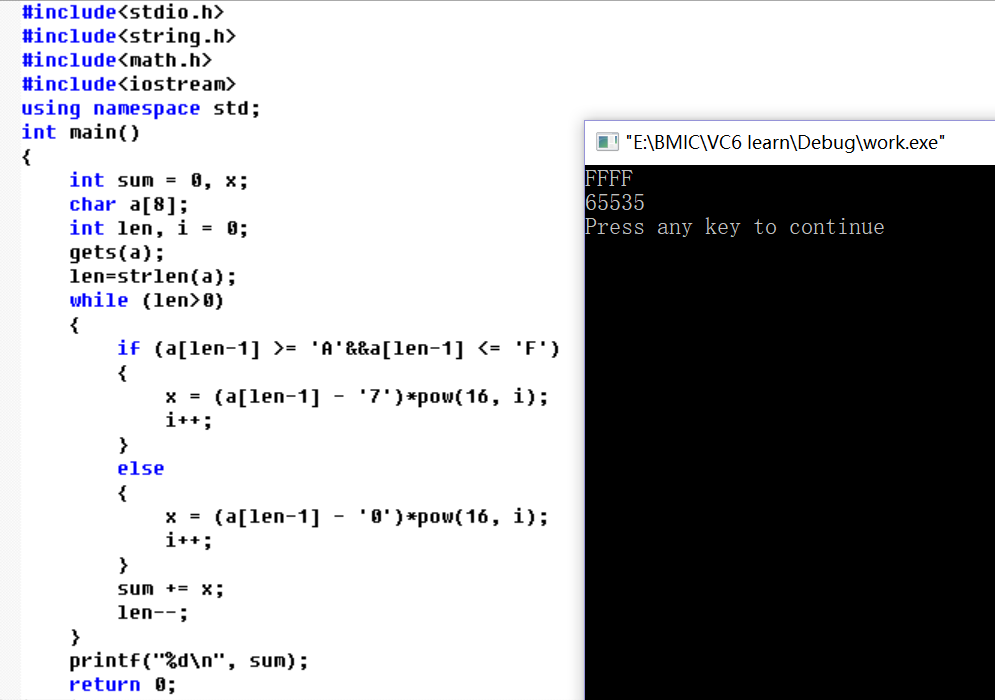
第二题利用数组存放字符串,可以用gets函数和strlen函数。strlen函数用来测量字符串的长度。A-F的ASCII码值是从65-70,若输入的为A-F则将其转化为10-15,可以用其ASCII码值减去“7”的ASCII 码数值刚好为10-15.若输入的是数字则ASCII码值范围是从48-57.令其减去“0”的ASCII码值得出0-9.再利用公式计算16次方。计算时倒序一次乘16的0次方,1次方···