11.27 Tues.
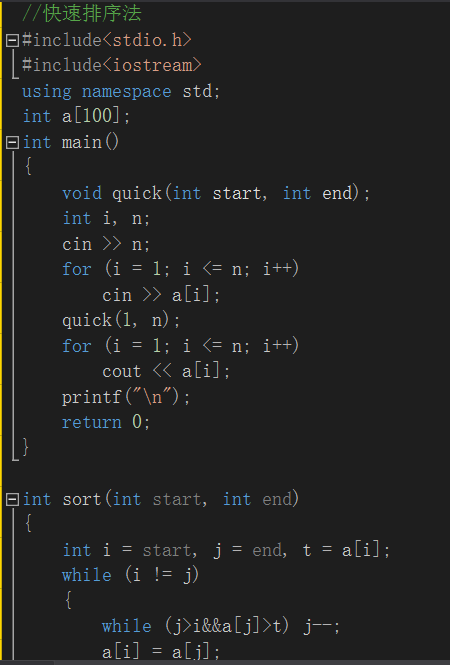
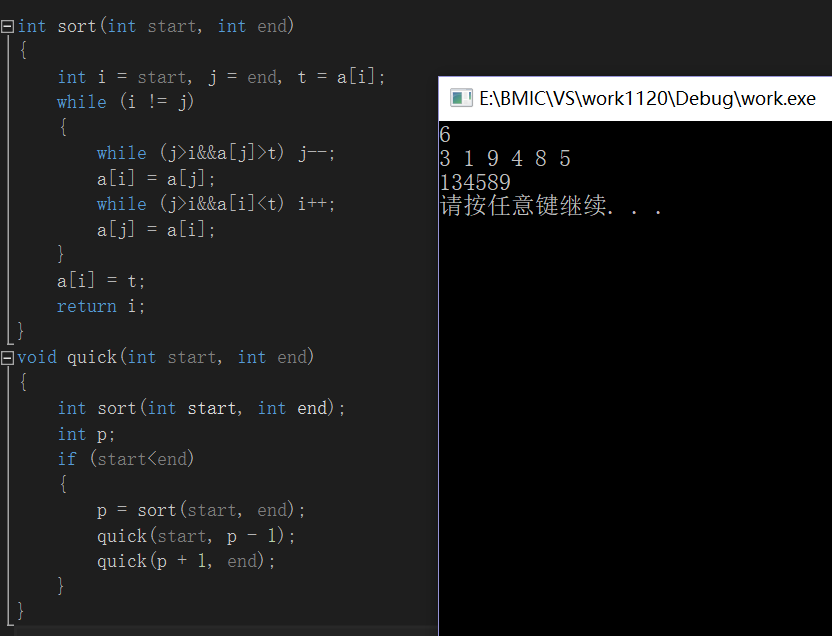
快速排序法:
i j
3 | 1 | 9 | 4 | 8 | 5 |
t=3
利用数组存放数据,然后选出一个参照数作为标准。例如:t=3,定义两个标记i和j分别从左右两端往中间走。若j所指的数小于参照数3,则放到3左边,同样若i所指的数大于3则放到3的右边,当i=j时,左边全为比3小的数,右边全为比3大的数。
i=j
1 | 3 | 9 | 4 | 8 | 5 |
t=3
这时3已经到达其在数组中正确的位置,再以3位临界点分别对左区间和有区间进行快速排序,以此类推···
当i=j时跳出循环,此时记录a[i]=t,t也就是下次分区间排序的一个分界点。
quick函数是分区间再次快速排序,quick(start,p-1)是从起点到分界点p的左边一个数排序;quick(p+1,end)是从分界点p的右边第一个数到末尾的排序。
数组a需定义为为全局变量
11.28 Wed.

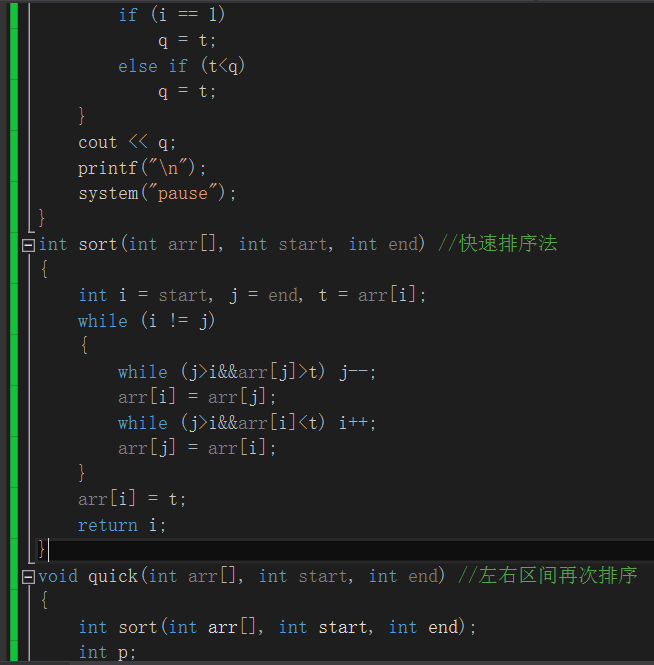
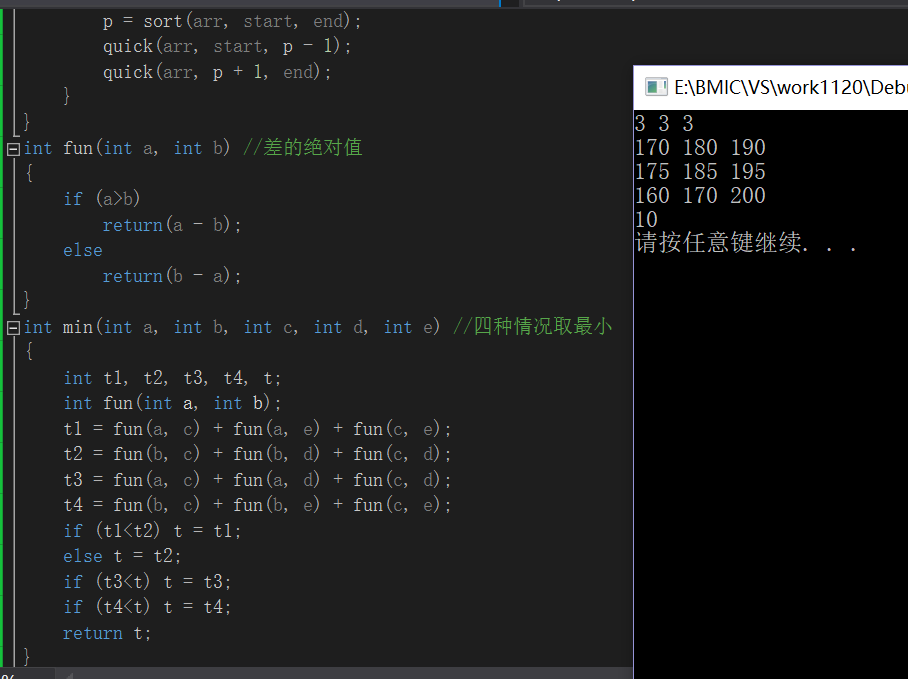
在昨天掌握快速排序的基础上做了上周的第四题:
思路:将输入的三个班级人的身高分别存入三个数组内并从低到高排序(调用函数使用快速排序法)。a、b都从第一个人开始,在a数组里寻找与b数组人身高最接近的两个人,同样在c数组里也寻找与b数组人身高最接近的两个人。这五个人分别有四种组合方法,取最小值并记录。b数组往后移一个人再进行这个过程,若存在D还要小的情况则记录下来,最后输出最小值D。
输完班级所有人的身高后利用快速排序法进行排序
查找计算过程:(主函数中第四个for循环)
第一步:i=1时,找到a数组中从1开始++,直到180>175,选取170和180;c数组中从1开始++,直到180>175,选取180和160。分别记为a,b,c,d,e然后存在四种组合情况:(a,c,e)(b,c,d)(a,c,d)(b,c,e)分别计算其身高差的和t1,t2,t3,t4,取最小值记为t
1
2
3
a[j]
170
a
180
b
190
b[i]
175
c
185
195
c[k]
160
d
180
e
200
其中计算绝对值调用到fun函数,在计算四种情况时调用到了min函数直接 计算并将四个比较大小返回最小值t。
第二步:i++后b[i=2]=185,此时:
1
2
3
a[j]
170
180
a
190
b
b[i]
175
185
c
195
c[k]
160
180
d
200
e
重复上面第一步的计算过程,再i++,直到b数组全部遍历。
主函数的if条件语句:i=1时计算出的最小值记为t,若i=2···后计算出的t比前面的t小则代替其值,输出最小的t。
作业:
第一题:
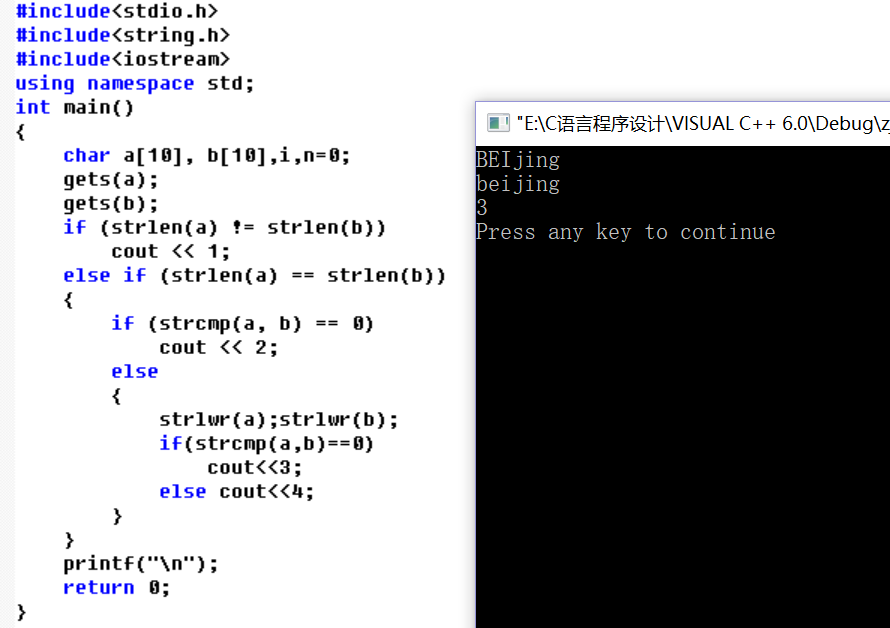
第一题用到一些有关字符串的函数会比较简单。分四种情况讨论:首先利用strlen比较字符串长度的函数判断一下是否两个字符串长度相等,若不相等则为第一种情况直接输出1;若长度不等则分三种情况判断:利用strcmp函数比较两个字符串的大小,若大小一样则两个字符串完全相同则为第二种情况直接输出2;若strcmp函数判断出来不相等,这时就表明剩下的两种情况,用strlwr函数将其转化为全小写,若转化后两个字符串完全相等则为第三种情况输出3,若仍不相等则为第四种情况输出4。
第三题:

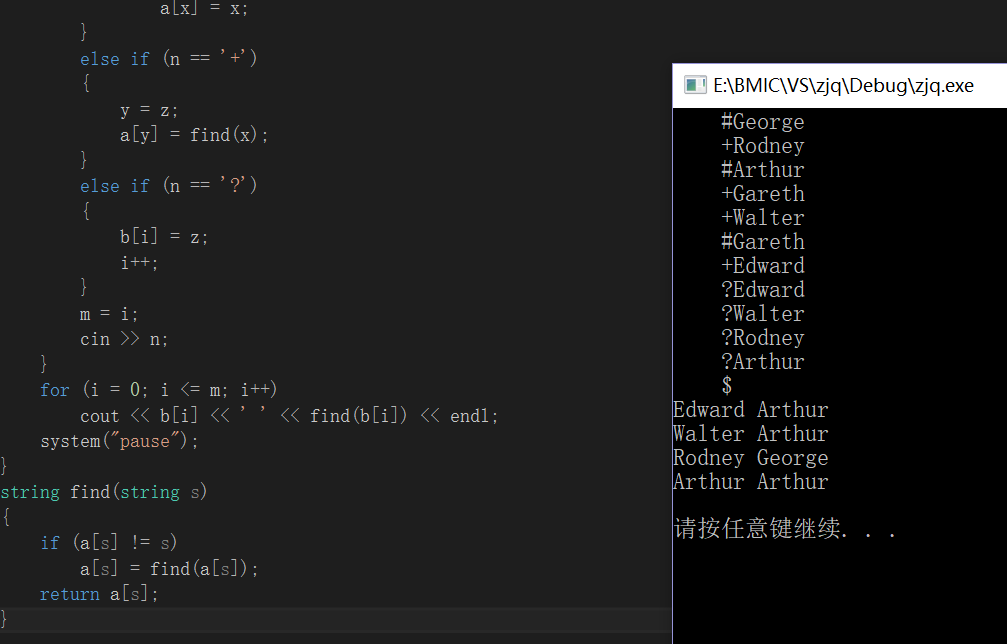
第三题仍是用到并查集的思想。但因为这题跟以往的做过的并查集的题不一样,这是不再是数字表示人物而是直接用名字,所以就要用到字符串。map<string,string>a就可以实现a[str1]=[str2]。为了输出形式方便同样定义的map<int,string>b以a[n]=str的形式来存入需要查找的人物关系并输出。再用并查集的思想判断根节点寻找根节点合并来处理。
用string型定义字符串x,y,z char型n定义前面的符号“#”“+”“?”或“$”
第一次输入n时while循环判断是否为$,不是则继续输入,否则停止。
while循环里面判断:
若n是#则后面输入的字符串z是父亲,但这时不确定他是否也是别人的儿子,所以做判断:x=z,若a[x]为空的话,则没有上级,它自己就等于本身,为最高级;
若不为空就证明还有上级。这里调用到并查集find函数,寻找根节点。
当n为+时,则为儿子,y=z,同样用find寻找根节点并令a[y]等于其根节点。
若n=?时,为了输出形式一起输出所以先把它存入map<int,string>b中a[0]=名字1,a[1]=名字2···
输出时就查找mapb中需要判断的人物,并用find函数查找上级,输出形式为cout<<b[i]<<’’<<find(b[i])
目前第三题还没有考虑到按照输入文件的要求和数据规模。
第二题:
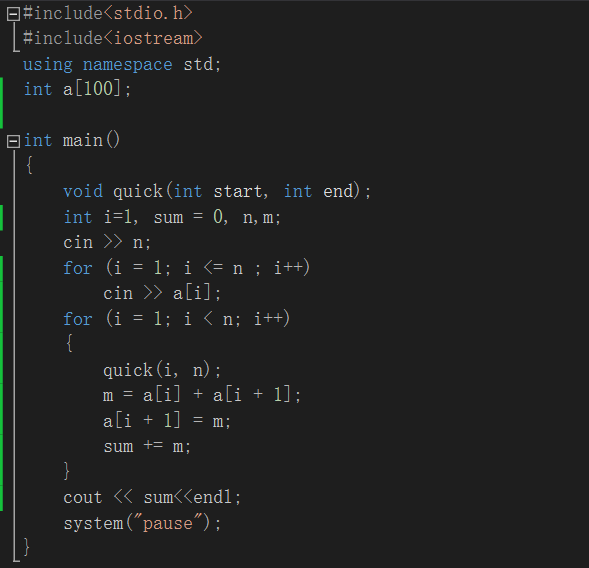
第二题思路:将数存入数组后用快速排序法进行排序,排序后为从小到大存放,可以从第一个数开始计算其与后面一个数的和,并代替其后一位数在数组中的位置。记录下此时他们的和为m。进行第二次排序,计算第二个数与第三个数的和,与上相同记录m后,m相加就是所求的sum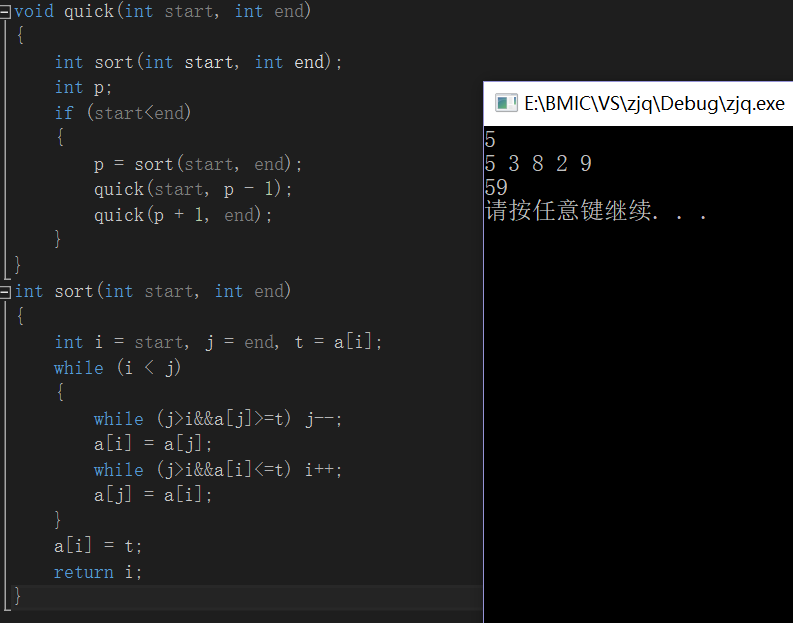
例:第一次排序后{2,3,5,8,9}
i=1时,a[2]=2+3=5;m=5,sum=5再排序
{2,5,5,8,9}
1=2时,a[3]=5+5=10;m=10,sum=5+10=15
以此类推···