朱清华
12.17:
过程:复习常微分+重做了一道C语言题目。
代码:
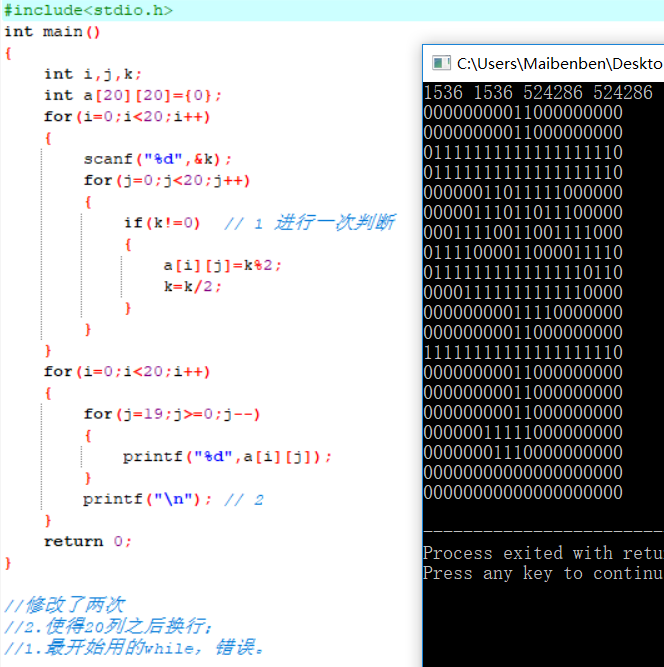
总结:
自己回过头来看这道题目时,做的更加顺畅一下。我在思考一个问题,能否直接让程序代码读入文件中的数据,避免繁琐的手动输入。带着这个问题,我决心好好地看看C语言的第十章(对文件的输入输出)。
对比复习了常微分方程的“一阶线性微分方程组”和“n阶线性微分方程”
(1)一阶线性微分方程组:
理解基础词汇的含义,通解——含有n个任意常数 C1, C2, ..., Cn的解;通积分——将通解带入原方程组,积分所得的方程组;朗斯基行列式——Yi (x)列向量组成的行列式。要能够熟练的运用所学的某类知识,必须先弄清楚相关知识的基本概念。
刘维尔公式:将朗斯基行列式与方程组的系数之间建立了相应关系。 应用的前提条件是,Yi (x)为齐次方程组的n个解值。
线性非齐次方程组的通解=其对应的齐次方程组的通解+一个特解。
(2)如何求特解?常数变易法!我的理解是:用Ci (t)将对应齐次方程组所求的基本解组,构造出非齐次方程组的特解,进而求导,得到纯量形式,再化简后积分,带入构造的特解方程,得到特解的值。
(3)对于常系数线性微分方程组的解法,与之前学习的线性代数紧密联系了起来。求其系数矩阵,通过|λ* E -A|求出λ的值,即特征根,判断单根还是重根。重根问题上,书本详细介绍了一种计算方法,P152。而对于单根,必须注意是否出现复数根。解决的办法,为欧拉公式:e(a+bi)x=eax cosbx+i*eax sinbx。
(4)n阶线性微分方程:基本解组——n个线性无关解。
关于特解的求解,除了常数变易法,掌握了一种新的方法——待定系数法(适用于某些情形)。关于其使用,应该先观察方程式的f(x)的形式,适合哪种情形,就选择对应的计算规则。
叠加原理:适用于f(x)为ex 类型和Ax2 +Bx+c类型同时存在。
12.18:
过程:自己动手制作了一个“米老鼠”的图案。知道了昨天那题如何高效的把数据制作出来。
代码:
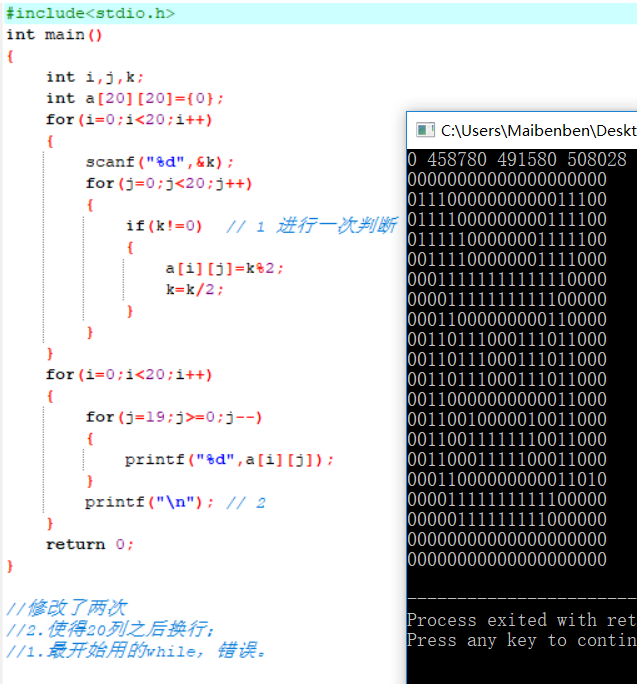
总结:
自己挺感兴趣这个题目,就继续思考了是如何将一个汉字,或者一个图案转换成二进制数。我自己想的办法是做出20*20的表格,将需要涂暗的区域,用1表示,这样,得出20行二进制数据。然后,分别转换成十进制。
显然,自己做出一个数字或者图案的方法,是很费时费力的。于是,我请教了学长。他是用“图像处理”。先截图一个汉字,做成图片。接着,使用MATLAB的功能,让图片转换成了1,0的矩阵(其中,1为白色,0为黑色)。最后,二进制转换成十进制。
RGB:red,green,blue(三原色光)
CMYK模式:与RGB相反,CMYK是一种减色模式,由青、洋红、黄、黑四色构成。CMYK是四色打印和印刷的基础,因此我们在最终输出作品时,都应该将图象转成CMYK模式。
12.19、12.20:
做数据,追神经元。
12.21:
看完了“对文件的输入输出”章节,了解了基本概念。fopen函数,打开数据文件;fclose函数,关闭数据文件。对于文件使用方式,注意是否有“b”。带有b的,为二进制文件;没有b的为文本文件。向文本文件输出时,遇到’\n’,会转化成’\r’和’\n’两个字符。而读入文本文件时,’\r’和’\n’两个字符会转换成’\n’。
文件打开之后,要进行读写——顺序读写,随机读写。前者容易操作,但效率不高。后者可以对任何位置上的数据进行访问。随机读写中,使用了rewind函数,作用是使文件中的文件位置标记重新定位于文件开头。
整体看完了,有点懵,不是很明确应该如何操作出来。这一章节,介绍了不少的函数,自己还要摸索的多实践几遍。
12.22:
过程:上午复习了离散数学中的“第五章,图的基本概念”,下午完成了之前的一道“最小身高”问题。
牢记基本概念:简单图——无平行边(注意方向性)+无环;平凡图——只有一个顶点+无边;空图——顶点集为空集(即什么都没有);零图——没有边的图(即仅有顶点)。
根据定义分析可知,平凡图是零图。但零图不一定是平凡图。
握手定理:(顶点度数与边的关系)=2m(度数:无向图中,顶点v作为边的端点的次数之和)
歌德堡七桥问题的证明,就运用到了握手定理。

我自己的思考是,学好图,很关键的就是如何从实际例子中提取出图的模型。比如,着色问题模型适用于排课表,安排时间开会,多人之间工作时间的分配等,这都是试图在存有冲突的情况下分配资源。很形象化的,点就表示工作,会议,人员,等实际的东西。而连有线的,就表示两者有关联。为了不引起冲突,有联系的必须涂不同颜色。这就构成了数学模型。
代码:
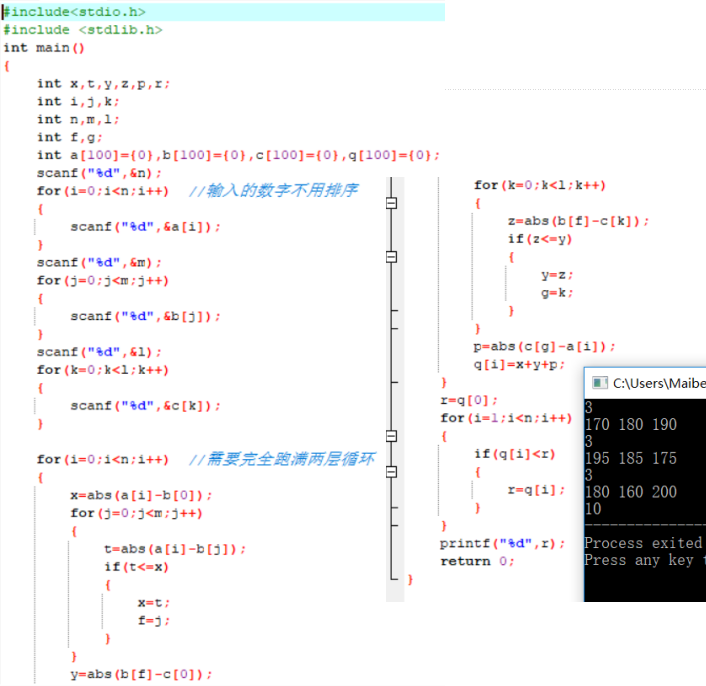
总结:
自己先用暴力的方法写了一遍,想着不需要排序。但是,修修正正了好多遍。出现的一些错误:1.循环嵌套了两次(实际,只用一次嵌套,但内层有两份);2. scanf忘记了&符号,搞得结果都没有显示,找了好几次,才发现这个问题;3.对B、C层找到的那个最符合的值的位置没有标记。总结来说,还是不够熟练,做的吃力,需要更加扎实自己的基础。
然后,用优化的方法解决,首先,A、B、C三层需排好序。再遍历B层,并分别从A、C两层寻找最靠近Bi 的两个元素,这样存在4种结果,比较得到最小的。代码运行了出来,也有了正确结果。和学长交流了自己记录的问题后,发现有几个点自己没有思考到,可以完善。1.排序问题上,自己思考了数组函数(冒泡,快排)和哈希表。但,最佳选择是快排(nlog2n)。冒泡时间复杂度为n2 ,会超时。而,哈希表因两类数据的数量级相差太大,即会出现太多a[i]=0(由数据范围太大,数据个数太小导致)。总结就是,哈希函数的规则是:通过某种转换关系,使关键字适度的分散到指定大小的顺序结构中。越分散,查找的时间复杂度就越小, 空间复杂度就越高。哈希查找明显是一种以空间换时间的算法。
很细节,但很重要的一个点,Bi 进行遍历时,只需要从Bi-1 遍历所得的那个较大的数开始比较寻找。后面,依次重复操作,直到结束。这个过程中,时间复杂度为n!!!
还有,while使用的方便,避免了每次都需要赋值i。While——通过每次对条件的判断,从而是否进行循环。